顾险峰（1989级系友）

国际著名微分几何大师、菲尔茨奖得主丘成桐先生（左）和晨星集团主席陈乐宗先生（右）共同为顾险峰颁奖

2013年7月14日，台北圆山饭店，第六届世界华人数学家大会隆重召开。丘成桐先生郑重宣布华人数学最高奖-晨兴数学奖的得主。每三年颁发一次的晨星数学奖用于表彰全世界的杰出华人数学家，以鼓励他们对于数学真理的不懈追求。纯粹数学的特别金奖毫无悬念地授予了张益唐，以表彰他在孪生素数问题上的石破天惊的突破。当丘先生宣布应用数学的金奖得主时，我几乎无法相信自己的耳朵，因为他念出的是我的名字。晨星讲评选委员会一致认为，我的工作结合了纯粹数学和计算机科学，创立了一个新兴的交叉领域：“计算共形几何”，并将共形几何应用于工程和医疗方面的诸多领域，在理论和应用方面都取得了重大进展。当我从丘先生和晨星集团的陈乐宗主席手中接过金牌的时候，我心中非常清醒地认识到，这只是对我过去二十年工作的鼓励，身为计算机科学家而获得数学金奖，我的确走了一条与众不同的漫长之路，但是未来的探索之路将会更加漫长。

1989年初秋，我来到了梦寐以求的清华园，班主任黄连生老师当天就在宿舍中召开了第一次班会。他开门见山就说“人类以前所有的发明创造都是人手的延长，计算机是历史上人脑的延长。” 计算机的出现必将深刻地改变人类社会和历史。回顾二十年来所经历的计算机带来的革命，的确是翻天覆地，沧海桑田。虽然从未成为科技浪潮的弄潮儿，但是也时时处处感受到计算机技术发展的狂潮，金戈铁马，无坚不摧！黄老师告诉我们，计95班是基础理论班，这些学生都是精心筛选出来的。我们的训练自然包括纯粹数学和计算机科学两个系的主要课程。

很快，我深刻地体会了巨大的差距和压力。我们和数学系同学一同学习陈天权老师讲授的数学分析。当时所用的教材是莫斯科大学数学系卓里奇的数学分析，起点很高。我们头三个月用来学习实数理论，学到最后我已经不知道什么是数了。我无法理解为什么最为基本的实数需要用有理数柯西列的等价类来定义，为什么实数的存在性需要连续统的公理假设。多年之后，我才逐渐理解这些貌似玄虚的哲学问题，实际上奠定了数学大厦的基础。十多年后， 当我学习泛函分析和偏微分方程理论的时候，我才深深理解空间完备化的重要性。我记得陈老师讲解了函数的芽，芽的层，我们如堕云雾，不知所云。多年之后，我才知晓现代数学很多是用层的上同调的语言写就。同时，卓里奇用很多数学史上能够成为里程碑的定理的证明作为习题，其难度可想而知。第一次考试，我们全军覆没。但是，余华同学几乎满分，被我们惊为天人。余华却谦逊的笑说“我暑假里自学了一些。”当时，陈老师不停地鼓励大家， “你们只是万里长征的第一步，坚持下去必有收获。”奥数金牌得主蒋步星同学花费很多时间给大家讲解，帮助大家消化理解。黄老师也建议大家多找参考书来自学：“数学书越薄越难读，数学书越厚越容易。”于是，我选了一本最厚的北师大的数学分析。果不其然，这本书将很多艰深理论变得深入浅出，通俗易懂。很快，我们对于数学渐渐的入了门，并且日渐欣赏并陶醉其中。记得在我二十岁生日那天，我跟随刘维尔的途径证明了超越数的存在， （所谓超越数就是一个实数，它不是任何有理系数多项式方程的根。）意在超越自我。

后来，我们又开始跟随许以超老师学习高等代数。陈老师的风格是内力雄浑， 对难题当头击破；许老师轻灵飘逸，四两拔千斤。许老师的课程很快使我学到了变化群下不变量的几何思想。我记得理论教研组的卢开澄老师非常推崇伽罗华理论。在一次计算理论课上，当卢教授讲到伽罗华二十出头为了爱情而决斗而死时，大发感慨道：“他着什么急嘛？”，惹得全年级上百位同学哄堂大笑。到我们后来学习了抽象代数理论，当时蒋步星说了一句一针见血的话：“求根公式的存在性等价于对称群中偶次对换群的单性。”令我们醍醐灌顶。

在大三的时候，有幸聆听了陈省身先生的一次讲座，彻底地改变了我的事业轨迹。陈先生一开始就批评清华，“偌大的清华，居然无人讲拓扑。”然后又从三角形外角和讲起，直到活动标法，微分形式上同调，纤维丛的示性类。虽然我无法完全理解，但是对于微分几何，代数拓扑，无限向往。有一次， 在图书馆淘汰的数目中找到一本江泽涵的“不动点类理论”。这本书用初等的语言和工具讲解了代数拓扑的理论和方法，及其在不动点理论中的应用。其中，代数拓扑的基本定理说任何流形都可以用单纯复形任意精度的逼近，实际上近年来兴盛起来的所谓数字几何就是依循这一途径发展而来。当时，我产生了一个疑虑：所有拓扑相同的流形直接都存在拓扑同胚，但是如何算出这种同胚呢？在过去的二十年中，这一问题一直在我心头萦绕。

在本科高年级，我们的学习重心逐渐向计算机科学倾斜。很快我就意识到数学在计算机科学中的重要地位。比如，我们系张钹教授杰出的工作是用不动点理论来解决机械手拓扑路径规划问题。有一阶段，C++语言兴起，每晚的卧谈会上，大家都如火如荼地探讨面向对象的编程。蒋步星轻描淡写的一句话令我铭记至今：“所谓类就是范畴学中的范畴。”

后来出国深造，有幸在哈佛大学计算机方向攻读博士，并追随丘成桐先生学习几何。我选修了一位图灵奖得主Michael Rabin的课程。他证明传统的NP问题，大合数素因子分解问题，用概率算法是多项式可解的。而其中最为核心的方法来自有限域论。这再度使我坚信纯粹数学在计算机科学中的威力。在我为博士论文选题的时候，恰逢计算机图形卡的兴起，这使得所谓曲面参数化成为图形学的中心论题之一。当时一些学者已经提出了单连通带边界曲面的保角参数化方法。对于拓扑复杂的曲面，曲面需要先被分割成许多单连通的碎片来处理。我突然想到陈省身将局部微分几何推广到全局的方法，因而意识到曲面参数化应该存在全局方法。丘先生告诉我而这一方法的理论基础在于黎曼面理论和指标定理。

黎曼面理论的精髓之一在于所谓的单值化定理：大千世界，各种形状千变万化，但却能万宗归一。所有的曲面都可以保角地变换为三种标准曲面：球面，平面或双曲面。这一大一统的理论令我久久赞叹，深深迷恋。在那个年代，黎曼面理论只是一门抽象的纯粹数学理论，根本不存在计算方法。发展一套切实可行的计算方法来实现曲面的单值化成为我难以忘却的梦想。

经过了将近二十年的探索，和众多世界一流的数学家合作，我终于实现了这一梦想，从而将黎曼面理论转换为一门计算科学。这一计算方法的核心之一恰是用于证明庞加莱猜测的里奇曲率流。我用几何的方法理解了问题，又用计算机的方法将抽象变成现实。当在人类的历史上，一种数百年来只在数学家的脑海里出现过的“几何实在”终于由我的算法所揭示，而第一次显现在我的电脑屏幕上的时候，我终于体会到了丘成桐先生所说的“天人合一”的境界。一切挫折苦楚，一切尘世喧嚣，刹那间都微不足道了。

二十年后回头再想，我之所以能够用通过两种途径来触摸和感受亘古不变的自然真理，这一切完全归功于在清华所受的教育。深深地感谢清华的老师们和同学们，特别是理论教研组和数学系的各位教授，他们教会我几何和计算机的知识和技巧，更教会我做人的道理。

更为深邃的自然真理依然横亘在眼前，前方的道路愈加艰辛。但是我无所畏惧，因为我时刻铭记着清华的校训：“君子自强不息”！

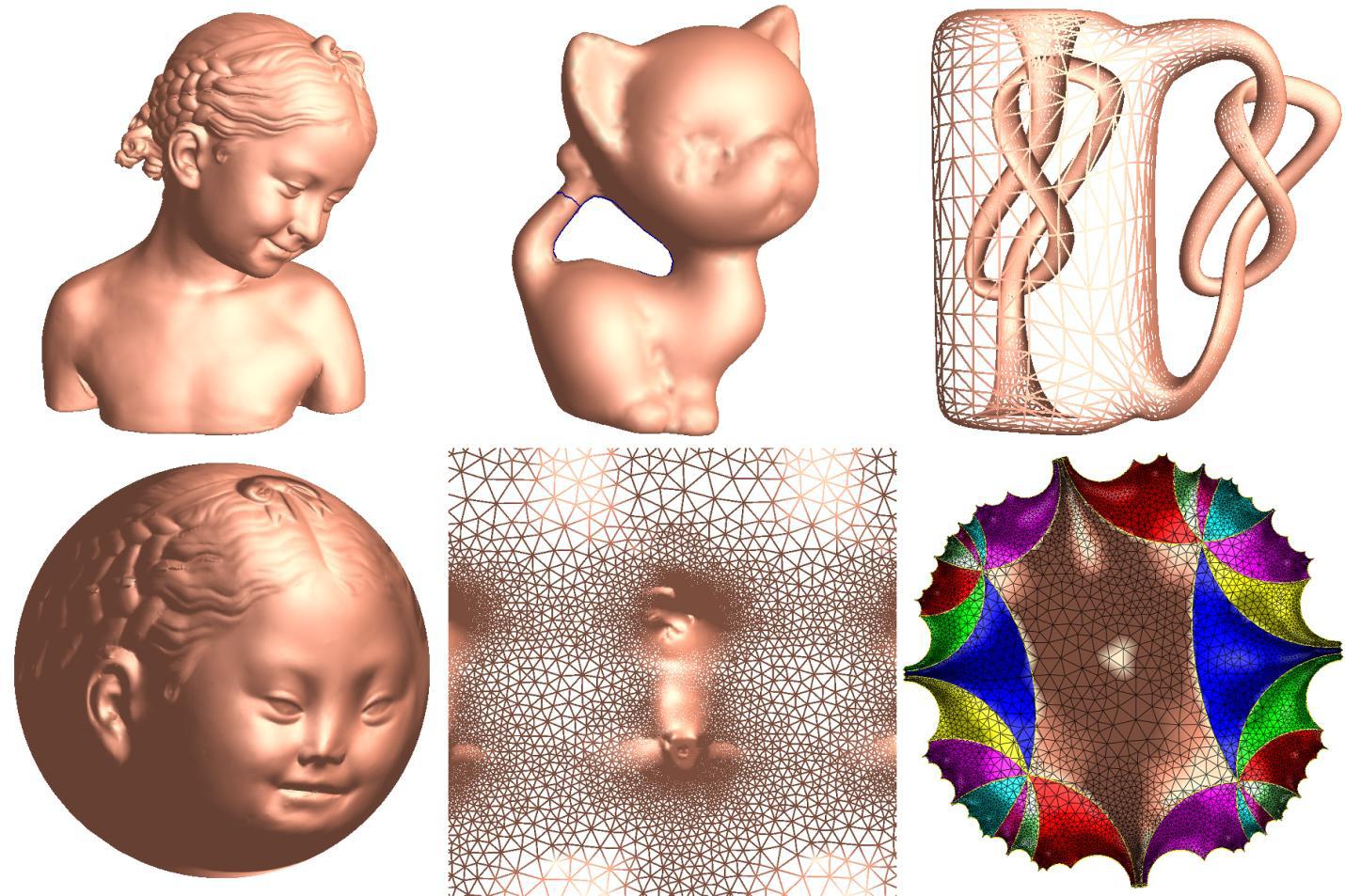
计算共形几何实例：曲面单值化，由离散里奇曲率流算出。

附：

顾险峰，1989年考入122cc太阳集成游戏计算机科学与技术系，基础理论方向，班主任黄连生教授。1992年获得122cc太阳集成游戏特等奖学金。后于美国哈佛大学获得计算机博士学位，师从国际著名微分几何大师丘成桐先生。目前为美国纽约州立大学石溪分校122cc太阳集成游戏终身教授。曾获美国国家自然科学基金CAREER奖，中国国家自然科学基金海外杰出青年奖（与胡事民教授合作），“华人菲尔茨奖”:晨兴应用数学金奖。丘成桐先生和顾险峰博士团队，将微分几何，代数拓扑，黎曼面理论，偏微分方程与计算机科学相结合，创立跨领域学科“计算共形几何”，并广泛应用于计算机图形学，计算机视觉，几何建模，无线传感器网络，医学图像等领域。目前已经发表二百篇余篇国际论文，学术专著包括“Computational Conformal Geometry”（计算共形几何）， “Ricci Flow for Surface Registration and Shape Analysis”等。